What is the Fry readability formula?
Fry is a formula used to calculate the US grade level required to understand a piece of text. This is the aim of most readability formulas. What makes Fry different from other formulas is how it calculates the grade level.
Fry is a graph-based formula. It uses sentences and syllables as variables. Fry plots the text on a graph, corresponding to the score. This was originally determined by sampling excerpts from texts. This was three sets of 100 words from. Then the average sentences and average syllables were taken.
These two figures were then plotted onto the graph. The intersection of the two lines is the approximate reading grade level of the text.
Where did the Fry readability graph come from?
The Fry readability formula was created by Edward Fry 1968. Fry contributed greatly to reading and readability research. He was president of the National Reading Conference.
Throughout his career, he became an authority on how people learn to read.
He also supported literacy development internationally. Whilst teaching in Uganda, he created Fry as a ‘formula to save time’. The graph promised ‘reasonable accuracy and uncommon simplicity’. He clarified that accuracy is within a grade level. This is useful for educators or librarians calculating reading age.
It also correlates well with other highly regarded formulas such as Dale-Chall, Flesch Reading Ease and Spache.
How is the graph calculated?
Fry’s graph was originally calculated as follows:
- Select three one-hundred- word passages from near the beginning, middle and end of the book. Skip all proper nouns.
- Count the total number of sentences in each hundred-word passage (estimating to the nearest tenth of a sentence). Average these three numbers.
- Count the total number of syllables in each hundred-word sample. There is a syllable for each vowel sound; for example cat, black-bird, cont-in-en-tal. Don't be fooled by word size; for example po-li-o, through.
- Endings such as -y, -ed, -el, or -le usually make a syllable, for example: read-y, bott-le.
- Count every syllable over one in each word and add 100. Average the total number of syllables for the three samples.
- Plot the average number of sentences per hundred words and the average number of syllables per hundred words. Most plot points fall near the heavy curved line. Perpendicular lines ark off approximate grade level areas.
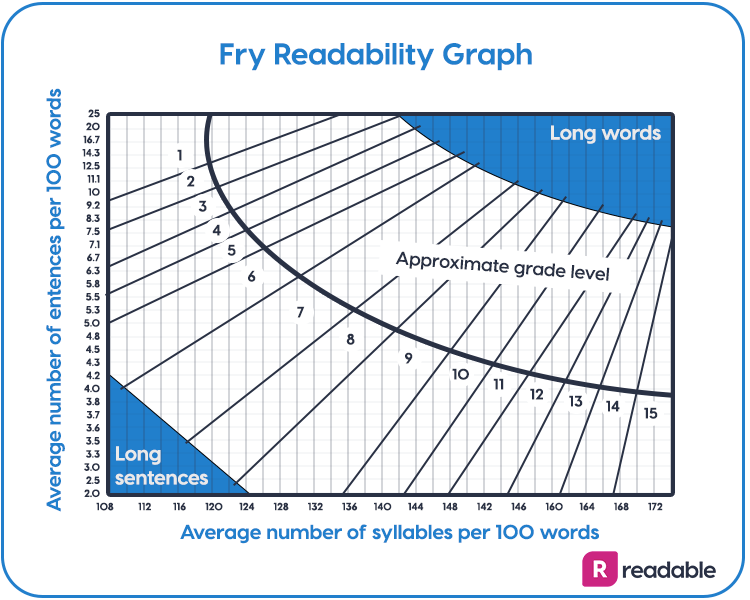
At first glance, this looks complex. But, it was an easier process than many formulas at the time. Luckily, it’s now even easier to calculate the Fry formula. Readable analyses the whole text. It gives you your Fry score as a US grade level within seconds.
When is the Fry formula most useful?
Fry himself pointed out many uses for Fry and other formulas. Among other uses, Fry can be used for:
- Libraries and schools
- Technical manuals
- Businesses
- Insurance
- Banks
- Advertising
- Publishing
- Law
- Healthcare
- Government
- Military
Unsurprisingly, the Fry formula is particularly useful in education. With a wide range of grading, it can be used for elementary to college level texts.
Real-world application
Fry is also one of several formulas used in healthcare. Clear communication is key - whether used within diagnosis or in ongoing correspondence. Studies have shown that patients who don’t understand health literature are less likely to follow instructions. They may therefore not fully understand their illness.
The Fry formula is also important in Law. Fry points out that the matter of readability has been pointed out in court cases. In his example, he discusses a court case regarding insurance policies. The claimant got nowhere near the payout they were entitled to because of the wording of the insurance policy. This was of particular concern because the claimant was elderly. Legal services pointed out that just under half the elderly population of New York had a less-than-ninth-grade education.
Edward Fry testified that their documents were written at college level. The insurance provider was undermining the rights of citizens to clear information. They had to take ‘prompt action’ to improve the readability of their documents.
For the same reason, readability has been discussed in cases regarding texts such as government documentation, private contracts and warranties.
How can the Fry formula help me?
Although especially useful for education, Fry has a wide range of uses. The Fry formula can tell you the grade level your audience have to be to understand your text. This can help you to clarify your writing, helping you to be clear, concise and readable.

